Rotate a shape about an arbitrary point

14 Mar, 2012 · by admin · Read in about 2 min · (426 Words)
canvas html5 javascript

I wrote this to answer a question on StackOverflow. It’s a piece of Javascript code to rotate an object around an arbitrary point. I underestimated the complexity of this problem and found no available solution online. To be honest, the objective is quite simple to achieve, but neverthless it made me review trigonometry and linear algebra and exercise the canvas API. Here is the original JSFiddle and this is the final result:

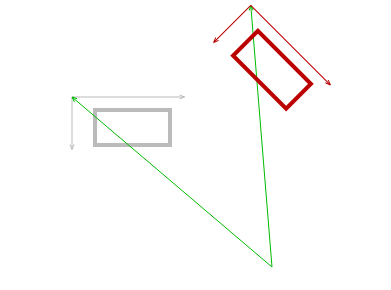
Rotate rectangle

Here the code

/*
 * This demo program draws a rectangle rotated
 * about a pivot point for the amount "gamma"
 *
 */
var context = document.getElementById("canvas").getContext("2d");
// rectangle's dimensions
var width = 75;
var height = 35;
// rotation angle
var gamma = 45 * Math.PI / 180;
// the pivot coordinates
var x = 200;
var y = 170;

// Some padding
context.translate(100, 100);

// Draw a rectangle in (0,0) and

function draw(color) {
    context.strokeStyle = color;
    context.lineWidth = 4;
    // Random offset
    context.strokeRect(23, 13, width, height);
    arrow(0, 0, width * 1.5, 0, color);
    arrow(0, 0, 0, height * 1.5, color);
}

function sqr(number) {
    return number * number;
}

function distance(x1, y1, x2, y2) {
    return Math.sqrt(sqr(x1 - x2) + sqr(y1 - y2));
}

// Draw an arrow from (x1, y1) to (x2, y2)

function arrow(x1, y1, x2, y2, color) {
    context.strokeStyle = color || "#0b0";
    context.lineWidth = 1;
    // draw the line
    context.beginPath();
    context.moveTo(x1, y1);
    context.lineTo(x2, y2);
    context.stroke();
    context.closePath();
    // draw the head
    context.save();
    context.translate(x2, y2);
    m = distance(x1, y1, x2, y2);
    sin = (y2 - y1) / m;
    cos = (x2 - x1) / m;
    alpha = Math.asin(sin);
    if (alpha > 0 && cos < 0) alpha = Math.PI - alpha;
    if (alpha < 0 && cos < 0) alpha = -Math.PI + Math.abs(alpha);
    context.rotate(alpha);
    context.beginPath();
    context.moveTo(0, 0);
    context.lineTo(-5, 2);
    context.moveTo(0, 0);
    context.lineTo(-5, -2);
    context.stroke();
    context.closePath();
    context.restore();
}

// Draw the base rectangle with grey
draw("#bbb");

// Rotate about an arbitrary point (red)
// 1. normalize
magnitude = Math.sqrt(x * x + y * y);
senA = -y / magnitude;
cosA = -x / magnitude;

// 2. compute the sin and cos of (alpha + gamma)
senAG = Math.cos(gamma) * senA + Math.sin(gamma) * cosA;
cosAG = Math.cos(gamma) * cosA - Math.sin(gamma) * senA;

// 3. Back to the old coordinate space
originTranslatedX = cosAG * magnitude + x;
originTranslatedY = senAG * magnitude + y;

// Draw arrows to show the rotation of the origin
// about the pivot point for the specified amount
arrow(x, y, 0, 0);
arrow(x, y, originTranslatedX, originTranslatedY);
context.save();
context.translate(originTranslatedX, originTranslatedY);
context.rotate(gamma);
draw("#b00");
context.restore();